Compass Bearings Hypothesis
Suns' Azimuth Hypothesis
Expansion-Contraction Hypothesis
Never Go Back Hypothesis
Hypotheses On Navigation By Migrating
Monarch Butterflies

Kiepenheuer and Schmidt-Koenig, Magnetoclinic
Hypothesis
Basic Idea:
Monarch butterflies Kiepenheuer
and Schmidt-Koenig magnetoclinic routes to the overwintering sites in Mexico.
Assumptions
- The only goal of the migrants is the overwintering sites in Mexico.
- The butterflies navigate in accordance with Kiepenheuer (1984) Magnetoclinic model as
follows:
- The butterflies have a sensor that detects the angle of inclination (dip angle) of the geomagnetic field.
- They actually perceive a "subjective" angle of inclination that is a function of the actual angle of inclination and the alignment of their bodies with the magnetic field (i.e. the direction that they are flying). .
- The butterflies prefer a particular "subjective" angle of inclination and navigate, in part, by flying in the direction that results in the perceived subjective angle of inclination equaling the preferred subjective angle of inclination.
- Because the angle of inclination of the earths magnetic field decreases as the butterflies fly towards the lower latitudes, they must shift their courses increasingly southward to maintain their preferred, subjective, angle of inclination. This behavior produces the curved route Kiepenheuer called a magnetoclinic route.
- The preferred, subjective, angle of inclination for monarch butterflies in North America is 73°12' (Schmidt-Koenig 1985, 1993).
Limitations of the Hypothesis
- Limited physiological evidence that monarch butterflies have sensors that can detect magnetic fields (However, see Jones and MacFadden, 1982)
- Because monarch butterflies are assumed to have a single, preferred, subjective, angle of inclination, there can be only one magnetoclinic route that actually leads to the overwintering sites) in Great circle Hypothesis.
- Boundaries of the geographic region where the hypothesis applies are not known. May not apply to western population (see Remarks in Great Circle Hypothesis).
- Isoclines of magnetic inclination are assumed to be smooth.
- Response of butterflies to changing angles of inclination are assumed to be uniform.
- Hypothesis does not explain why migrants turn SSE when reach about Longitude 100° to 102° in northern Mexico.
Advantages of navigating by following a Kiepenheuer and Schmidt-Koenig magnetoclinic route
- The single 'true' magnetoclinic route is similar to the Great Circle route from approximately the center of distribution of the eastern population in late summer, the Great Lakes region in late summer, to the overwintering sites and can serve as the basic, or backbone (Kiepenheuer 1984), system for navigation.
- The ability to determine the magnetoclinic route should be independent of cloud cover.
- The spring return migration can follow the magnetoclinic route to navigate back to the Great Lakes region.
Problems of navigating by following a Kiepenheuer and Schmidt-Koenig, Magnetoclinic Route
- The true magnetoclinic route from center of distribution of the eastern population crosses a large section of the Gulf of Mexico.
- Butterflies that don't begin their migration at some point along the true magnetoclinic route, or are blown off course, are lost and will miss the overwintering sites entirely unless they have other, backup, methods of navigation.
- Migrants must continuously adjust their heading to remain on course.
- Flying high and soaring in thermals must be restricted to direct tailwinds to the magnetoclinic route.
- The magnetoclinic route between two points is generally longer than the corresponding Great Circle route.
- Magnetic field precesses fairly rapidly in evolutionary time so that populations must experience continuous natural selection to track changing magnetic coordinates.
Problems in Testing the Kiepenheuer and Schmidt-Koenig Hypothesis
- Predicted bearings for Magnetoclinic routes are similar to Great Circle routes for a large section of the range of the eastern population
- The geographic boundaries of the region in which the hypothesis applies are not defined.
A Test of the Kiepenheuer and Schmidt-Koenig Hypothesis
Predictions
- Preferred directions of migrating monarch butterflies at observation sites are identical to local Kiepenheuer Magnetoclinic routes based on a 'subjective' angle of inclination of 73°12'.
- Mean directions of migrating monarch butterflies at observation sites are identical to local Kiepenheuer Magnetoclinic routes based on a 'subjective' angle of inclination of 73°12'
Methods
- Determine the bearing for the Magnetoclinic route from the field site based upon a preferred subjective angle of inclination of 75°12'.
- Record at least 25 Category I, 50 Category II, or 100 Category III vanishing bearings of migrating monarch butterflies. Categories II and III vanishing bearings should be obtained over a wide range of wind conditions.
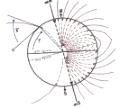
- Plot the data as a Rose Diagram (a circular histogram). See the "Methods for Observing Migrating Butterflies" section of the Red Admiral and Painted Lady Web Site for an example of a Rose Diagram. A string of dots, with each dot representing a single observation, can be used in place of bars
- Calculate mean vector (mean vanishing bearing ) as shown in Batschelet (1981) or Zar (1996) and add to Rose diagram.
- Use Rayleigh test in Batschelet (1981) or Zar (1996) to test test if mean vector is significant. Proceed with analysis only if mean vector is significant.
- Calculate the bearing for the K/S-K magnetoclinic route (Kiepenheuer, 1984) and add to rose diagram.
- Look up 95% Confidence Interval for mean bearing in Batschelet (1981) or Zar (1996).
- Indicate the boundaries for the 95% confidence limits on the Rose diagram (i.e.equal to mean bearing ±95% C.I. interval).
- Examine the Rose diagram. If the data are obviously skewed to one side, or bimodal (two peaks), you should not proceed with analysis. Data analysis to this point has been a standard exercise in descriptive statistics. More complicated procedures are necessary to continue. If data are not obviously skewed or bimodal, proceed to Decision Rules.
Decision Rules
- If bearing for Magnetoclinic Route falls within the arc delineated by the 95% confidence limits for the mean bearing (mag.), than the two bearings are not significantly different and the hypothesis cannot be rejected.
- If the bearing for the Magnetoclinic route does not fall within the arc delineated by the 95% confidence limits for the mean bearing (mag.), than the two bearings are significantly different and the hypothesis is rejected.
Remarks
This hypothesis was advanced for monarch butterflies by Schmidt-Koenig (1985, 1993).
The Kiepenheuer and Schmidt-Koenig (K/S-K) magnetoclinic hypothesis is similar to the
Great Circle hypothesis in that both predict specific preferred directions for migrating
monarch butterflies if certain information is  known. If the preferred, subjective, angle of
inclination is known for the butterflies, and the inclination and declination of the
magnetic field are known for the field site, then equation (2) in Kiepenheuer (1984) can
be used to calculate the predicted preferred direction. Conversely, if the preferred
direction of the butterflies is known, and the inclination and declination of the magnetic
field are known for a field site, then equation (1) in Kiepenheuer (1984) can be used to
calculate the preferred, subjective, angle of inclination of the migrants. If, at some
point in the migration, the preferred, subjective, angle of inclination of the butterflies
changes, then equation (1) would provide the new value.
known. If the preferred, subjective, angle of
inclination is known for the butterflies, and the inclination and declination of the
magnetic field are known for the field site, then equation (2) in Kiepenheuer (1984) can
be used to calculate the predicted preferred direction. Conversely, if the preferred
direction of the butterflies is known, and the inclination and declination of the magnetic
field are known for a field site, then equation (1) in Kiepenheuer (1984) can be used to
calculate the preferred, subjective, angle of inclination of the migrants. If, at some
point in the migration, the preferred, subjective, angle of inclination of the butterflies
changes, then equation (1) would provide the new value.
There have been no further papers published on tests of the K/S-K magnetoclinic hypothesis for monarch butterflies. As an exercise, I calculated the eventual destination of migrants from Mississauga, Ontario, based upon a preferred, subjective, angle of inclination 73°12'. I assumed that they flew at a constant speed of 5 meters per second (18 km/hr) under conditions of no winds, and recalculating the preferred direction every six hours in accordance with the new values for the inclination and declination of the magnetic field. The K/S-K Magnetoclinic Route from Mississauga, Ontario, would have taken the butterflies very close to the overwintering sites. This result is intriguing because the lower Great Lakes region has been considered to be the center of distribution of the eastern population in late summer when the migration begins, However, the magnetoclinic route crosses a section of the Gulf and the length of the crossing is much greater for butterflies that start from sites located to the east of the calculated route. Apparently, the K/S-K magnetoclinic hypothesis is incomplete.
The western population of monarch butterflies presents some of the same problems for the K/S-K magnetoclinic hypothesis as for the Great Circle hypothesis. As was the case for the Great Circle hypothesis, the coastal overwintering populations can be explained as: (1) a range contraction, (2) an inappropriate expression of the eastern migration pattern by butterflies that are 'unaware' of their western location, (3) an appropriate expression of a facultative adaptation of the North American population to the existence to two possible overwintering sites in North America, or (4) a local adaptation by an isolated population.
Please Submit Data with Tactics and Vectors Archives
Please send copies of all data and data analyses to Tactics and Vectors for
inclusion in the Archives. Your data should deposited in the Archives even if mean vectors
were not significant. Nonsignificant data is important information and can be used to
discriminate among different theoretical models. Further instructions may be found in How
to Submit Data to Tactics and Vectors (UNDER CONSTRUCTION).